Summary

In this comprehensive study, most bikes, but especially folding bikes and soft tail bikes, are found to be too soft for optimal pedaling speed–some seriously. A method to measure stiffness is proposed. The theoretical calculation of deformation energy is compared with various forms of experimental results. Improvement suggestions and their verifications are presented.

Recent studies at DAHON showed that frames of most bikes and some E-bikes, but especially folding ones and most soft tail MTB’s are in need of added stiffness in order to optimize pedaling efficiency (by as much as 40%), etc. Many people have studied bicycle frames from different perspectives and have speculated on the importance of stiffness in bike frames. In this study here, we attempt to give a “comprehensive, scientific” and yet practical discussion on the subject in general. A series of 4 articles will hopefully be published in 2023, respectively titled:

1. The folding bike: problems and solutions, (presented below)
2. Bike stiffness vs. peddling efficiency
3. Optimization of bike frame designs
4. Performance of improved frames.

1. The Folding Bike: Problems and Solutions

However, even most hard tail bikes today, while being quite stiff in the vertical plane, tend to have too much lateral flexes – often in the interest of lightweight, styling and cost-effectiveness. And perhaps, a kind of "trending" in the industry. This has led to unnecessary energy wastage during peddling, which should be intended solely for propulsion. The use of the word "wastage" is based on the principle of conservation of energy in physics. Claims of efficacies of a certain amount of frame softness (opposite of stiffness) are not necessarily unfounded, but they are mostly anecdotal, and thus remain questionable. Propulsion efficiency must remain paramount for bike designers. In our view, bikes of most categories, excepting perhaps BMX, should be re-examined for peddling optimization. Folding bikes are focused in this first article.

The first exceptions to the principle of triangulation really came last century with the emergence of folding bicycles – in the interest of easier storage and portage. Instead of a front triangle, a single large tube began to appear to link the bottom bracket (where the propulsion force is applied) with the head-tube (which controls the front wheel). (The rear triangle is sometimes simplified too). If this single-tube is very strong and sturdily welded, then it can provide a serviceable bike, though much heavier and perhaps less safe. In recent decades, folding bike has become very popular in some markets. As the market went after lightweight and compactness, as well as cost competitiveness (ouch), safety and performance are somewhat compromised — as attested by not-a-few complaints/recalls. (Most soft-tail MTB’s today suffers from too much compromise of the rear triangle – even when "locked".)

When we first designed the DAHON folding bikes 40+ years ago, they all had front triangles. (Figure 1) (second-hand versions of these are still available online). But by ~1996, we began to yield to the simpler approach of a single-tube – for expediency. (Though, as the oldest supplier (40 yrs), DAHON's ~ten million rigorously designed/built/tested products –– are still considered among the best and safest).

Nonetheless, as more and more "cheap" DAHON copycats surface everywhere, an uneasy feeling grew. Recently, we finally conducted a lot of experiments and analysis. And, without reservation, we concluded that single-tube bikes and e-bikes should return to the traditional front and rear triangles. It is not just the crucial safety issue alone, but other vitally important issues emerged as well.

STIFFNESS OF FRAMES

Stiffness (as opposed to strength) of any bike is important for peddling efficiency, especially for going up hills or trying to get ahead. It can be defined by the amount of limited deformation or flexes under the force applied to the pedal when the tires are virtually and momentarily "fixed" on the road surface. Many components contribute to this flexing: tires, their cross-section and pressure, the rim sets, the forks, the cranks, and eve the handlebar system and the seat-post, to some extent. And then, most significantly, the frame itself! The energy in causing these deformations is mostly irretrievably lost from the basic purpose of propulsion. Compared to a good traditional frame with a front triangle, a single-tube folding frame yields more flexes under load – unsurprisingly!

How to define and measure the stiffness of a frame is not a trivial question. Many have tried. First, we have to define quantitatively "frame deformation" which is actually distributed, and energy stored, throughout the many tubes. Fortunately, most of these tubes are connected directly or indirectly to the BB tube. Since the solid BB tube is where forces are being applied, we can conveniently observe its displacements. In our modeling, we propose to measure the observable displacements of the BB as a definition of the totality of deformation energy – to be tested experimentally.

Like any solid body in physics, the BB has 6 independent degrees of freedom, typically in terms of the orthogonal X, Y, Z (linear), and A, B, C (angular), as shown in figure 3. Obviously, displacement in the Z-direction is negligible due to the lack of an applied force component in the test; and C is zero on account of the BB’s bearings. So, 4 distinct dimensions of deformation exist and are recorded, from a force applied to the pedal. The first pair of deformations is in terms of the temporal X and Y displacement of the center of gravity of the BB tube; the second pair is the rotations of the BB tube, represented by angles A and B, around a front-rear axis, Z, and B, around the vertical axis, Y, respectively. These 4 dimensions of deformation are "linear" by definition of classical physics (ones that are proportional to the applied force, returning to the original positions without permanent deformation once the applied force is removed). These degrees of freedom and deformation are largely independent and must be considered separately, and their stored energy additively, again according to classical physics. (Small cross terms may exist, but these are neglected for the purpose of this study).

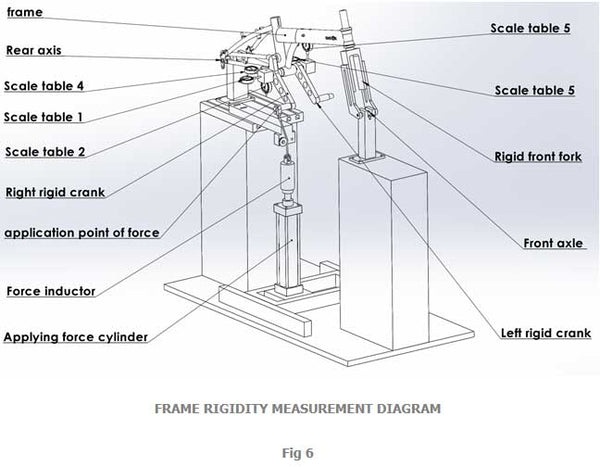
Experimentally, figure 3 4 and 6 illustrates how 45 bikes of different types have been tested using a modified CEN testing platform in which both the front fork and the cranks are solid steel.

Eight representative types of frames have been tested:

• BMX frame
• 2–4 Popular single-tube folding bikes
• Popular road bikes
• Popular MTBs
• Dual suspension/soft tail bikes
• A single-tube folding bike reinforced with a DELTEC steel cable, which connects the front of the single tube to the bottom bracket, thus forming a "front triangle" in the plane of the bicycle

Figure 6 shows a semblance of CEN testing equipment. What is not shown is that the frame is mounted differently, by having the front and rear axles constrained from vertical and the X-direction motions only. And they are otherwise allowed to move in the horizontal plane linearly in the Z direction and angularly – to approximate actual riding situations. (Fixing the axles solidly would erroneously increase the rigidity.)

A force F is applied to the center of the pedal at inclinations angles = 0, 10° and 20° from the vertical plane These angles are to represent common frame inclinations (sways) at different intensities of pedaling, including going up-hills or dashing for the finish line. The linear and angular displacements of the BB are recorded, to be correlated to various inputs of F.

Since there should be no permanent deformation, so according to classical physics, each of the 4 degrees of deformation obeys, for example:

where, representing the 4 degrees of freedom, X is the deformation displacement, KX is the stiffness constant (Young's Modulus), and FX is the X component of the force applied onto the pedal.

The 4 Stiffness Constants can be calculated if we know the applied forces and torques in the 4 dimensions, X, Y, A and B, along with their respective displacements. And we do, from the experiment. Let us define some terms based on figure 4:

LP= distance between the center of gravity (CG) of the BB and the center of the pedal.

LCR= distance between the CG and the chain ring;

LR= radius of the chain ring;

LC= length of the crank;

L= distance between CG and the crank;

B= 20°, which is the angle of inclination of the bike;

C= the angle of the crank from the horizontal plane;

TZ= torque applied on the BB around the Z-direction;

TY= torque applied on the BB around the Y-direction.

The various forces and torques are calculated as:

where C is 45°in this experiment.

The total energy of deformation, including all 4 dimensions, is:

where, according to eq. (1), the stiffness constant can be obtained experimentally like:

The various displacements are recorded and presented in table 1. Using the general formula of equation 3, one can easily derive the 4 stiffness constants, which are presented in the same table.

Forty five bikes from the market were tested. Table 1 presents 8 representative bikes – in descending order of stiffness.

ENERGY WASTAGE FROM FRAME DEFORMATION

We illustrate this stiffness issue with the case of a bicycle straining up a steep hill. Let’s calculate the frame deformation energy, E, in one pedaling cycle. We assume that the bike sways plus or minus 20°, without caring about the details of pedaling. According to eq. (3), the stored energy at any time t is:

The frame goes through an oscillation between 2 maxima synchronized with the pedaling cycle. For instance, in the X direction, the maxima, XM, is in the left and right directions. The same analogous behavior goes with the other 3 degrees of freedom. So each degree of freedom goes through a roughly sinusoidal movement between 2 maxima. Thus, in the case of the X direction,

The energy of deformation in the X direction at time t, according to equation 3, is:

The total energy expended in the X direction, ECX , in a pedaling cycle, is equal to the average, <Ex (t)>). Thus:

where P is the period of 1 cycle of pedaling; and the 2nd from the last "=" sign is according to a familiar formula in calculus. And the average energy in frame deformation in the X direction is therefore equal to:

And, for all four degrees of freedom, the total wasted energy in a pedaling cycle is:

All these values are found experimentally. As an example, based on these results, a rider weighing 90 kg, with bikes and accessories weighing 15 kg, riding up a steep hill, swaying the bike +/-20°, would expend 11 joules of energy in flexing the frame per complete cycle of pedaling. This is calculated and displayed in the same Table 1 for comparison and contrast.

The energy wastage (EC in table 1) in deforming the frame in one pedaling cycle gives you a measure of the stiffness. The greater the wastage, the lesser would be the stiffness. If one carefully reviews these comparative results, significant conclusions can be drawn:

1. Small wheels and frames as well as triangulated frames are stiffer; steel material is stiffer. (Wheel and front fork stiffness are excluded here, the inclusion of which would further change the results in favor of smaller wheels and frames.)
2. The DAHON fortified with a Deltec cable surprisingly stands out to be the stiffest among all samples, including big wheeled road bikes and BMXs, except for BMX. Deltec apparently is a sufficient quick fix for single tube folders. It improves the stiffness by 16% in the current scenario. Long-term, a fully triangulated foldable frame might be preferable if cost allows.
3. Many hard tail Road bikes are found to be surprisingly soft– as much as 10%-12% softer than the DAHON Deltec’ed sample! In general, big wheel/frames bikes require much more attention in the future.
4. The Soft tail MTB is softer than a Deltec’ed DAHON by as much as 20%-25%. Why? It is found that a genuine rear triangle is significantly compromised, causing serious flexibility between the BB tube and the rear axle. (That is one reason why the axles must be conditionally free to move in testing experiments for frame stiffness).
5. In particular, the folding bike by BrX stands out as softest. It wastes 56 times more energy as a Deltec’ed DAHON. Reason? On top of replacing a single tube for the front triangle, and a consequential compromise in the "rear triangle", its rear suspension's pivot is positioned uniquely and exceptionally low, causing the bike to bop seriously while pedaling hard.
6. In a complete pedaling cycle, the wasted energy in a soft bike can be as much as 11 joules (NM), which is like lifting 1.1 kg for one meter. Assuming a nominal pedaling cadence of 90/min, that is 990 J/min (almost like lifting 100kg–more heavy than most cyclists– for 1 meter per minute!

These theoretical results are corroborated with road tests/competitions and roller tests, as well as computer FEA. These will be reported in subsequent articles.

DURABILITY

Other than wasting pedaling energy from frame softness, folding bikes have other issues to resolve.

Gradual loosening of the folding hinge systems are all too often complained with cheaper products. The folding hinge of a single-tube folder is typically situated halfway between the front and rear wheels, taking on 5-10 times the weight of the rider in the form of a flexural or bending force during a ride. This constant abuse can gradually loosen the hinge system, both with its latching device (quick release) and with the axle hinge itself. In frequent use, the latching device needs to be adjusted from time to time (a nuisance). And the axle hinge itself, once loosen, will stay loose, and causes annoying noises. It may eventually limit the longevity of the irreplaceable folding hinge system, and thus the bike itself.

In a triangulated folding bike, however, the tensional force is either on the down-tube or the Deltec cable, as the case may be, while the top tube, along with the folding hinge system, would experience mostly compressional force. See figure 7. The folding hinge is therefore spared from any major amplified flexural forces. It would thus stay firm and adjusted, and no annoying noises will ever develop. The folding hinge in the down-tube or the Deltec cable does experience nominal tensional and torsional forces and expected to survive easily if adequately built. But longevity can be overshadowed by another issue, that of safety.

SAFETY

In most folding bikes, the folding systems (hinge), midway between the front and rear wheels, nowadays are welded to the oversized single tube by bud welding by TIG (as opposed to brazing). Structural stress concentration at the weld is therefore inevitable. Besides, the welding heat zone typically suffers metallurgical metamorphosis which tends to weaken the alloy material, often significantly. Not to mention occasional "fake welding". Obviously, the combination of the these factors does not help safety at all. Failures occurring in this region with cheap folders is no big news anymore. Moreover, single-beam folding E-bikes, with their heavier weights and higher speeds, conceals even more danger. See figure 8 broken frames

Fortunately, several folding frames equipped with Deltec have been tested to more than a million cycles, 10 times the requirement in most international standards! That included a few cheap folders off-the-street that are otherwise seriously substandard by themselves. Deltec’ed DAHON models are now regularly tested with 50% heavier loads and they survive way beyond normal standards.

CONCLUSION

1. All bike categories except perhaps for BMX need to be re-examined for propulsion efficiency. DAHON has made some initial moves. We hope the rest of the industry would also be alerted, and to excel themselves for their consumers" solid needs.
2. Folding bikes and e-bikes should adopt or re-adopt the “safety bicycle” teaching of triangulation (with bona fide front and rear triangles), to provide the public with better riding speeds, durability and, most essentially, safety. It is technically feasible with marginal additional costs. As such, folders may finally be the superior products they can be in many categories, on account of their added values in portability and storability.
3. For other related topics, please watch for the rest of the articles mentioned at the beginning of this article, viz:
1. Bike stiffness vs. peddling efficiency,
2. Optimization of bike frame designs,
3. Performance of improved frames

David T Hon, PhD., CEO, DAHON, was Assistant Professor of Physics, California State U, Pomona; Senior Physicist, Hughes Aircraft Research Labs, Malibu; co-author of professional reference "Laser Handbook" (North Holland Press, 1979); his invention "SBS phase conjugated reflection in a tapered waveguide" in 1982 is still widely used in high-power lasers, including laser fusion programs today. He is inventor or co-inventor of 500+ patents across 4 fields, 20% still active. Moe Moses, Senior Engineer, DAHON, inventor or co-inventor of dozens of patents.

*We thank our DAHON colleague, Dr. Hubert Songster, for graciously and carefully checking our calculations.